 3log1/2x+5log1/2x-2. Решите уравнение log 1/2 1/4 +log 1/2 2. Log2x>1. Log2x 3 x 2 1. Log2x>1.
3log1/2x+5log1/2x-2. Решите уравнение log 1/2 1/4 +log 1/2 2. Log2x>1. Log2x 3 x 2 1. Log2x>1.
|
 Log неравенства. Решение log3(x-2)=log3(2-x). Лог 1/2 2х+5 -3. Log2x<1/2. Log1/3(2x+1)>-1.
Log неравенства. Решение log3(x-2)=log3(2-x). Лог 1/2 2х+5 -3. Log2x<1/2. Log1/3(2x+1)>-1.
|
 Log2x 3 x 2 1. Log4 x 2 x 3 log4 x-2/x-3 2. Лог 3 5 лог 3 7 лог 7 0. Log5 3x+1 2. Решите неравенство 〖log〗_|x-2| (x^2-1)≤2.
Log2x 3 x 2 1. Log4 x 2 x 3 log4 x-2/x-3 2. Лог 3 5 лог 3 7 лог 7 0. Log5 3x+1 2. Решите неравенство 〖log〗_|x-2| (x^2-1)≤2.
|
 Решить неравенство log2x>-1. Решение уравнение log3(x-2)=2. Log5 7 x log5 3 x +1 одз. Log2x 3 x 2 1. Log2x.
Решить неравенство log2x>-1. Решение уравнение log3(x-2)=2. Log5 7 x log5 3 x +1 одз. Log2x 3 x 2 1. Log2x.
|
 Log2x 3 x 2 1. Log2(x-1)+log2x<1. Логарифмические неравенства. Log2x 3 x 2 1. Log2x>0.
Log2x 3 x 2 1. Log2(x-1)+log2x<1. Логарифмические неравенства. Log2x 3 x 2 1. Log2x>0.
|
 Log2 x log2 x-3 +1 log2 x 2-3x. Log x 2x-1 log x 2x2. Log7(x+3)=2. Метод введения новой переменной логарифмические уравнения. Log x 2 x+1 2 1.
Log2 x log2 x-3 +1 log2 x 2-3x. Log x 2x-1 log x 2x2. Log7(x+3)=2. Метод введения новой переменной логарифмические уравнения. Log x 2 x+1 2 1.
|
 Log5(x+1)+log5(x-1)=3log5 2. Решение неравенства 1/2 log2(x 2-1)>1. Лог 2 2x+1 лог 2 3+1. Log2x<1/2. Решить неравенство log3 x+2 3.
Log5(x+1)+log5(x-1)=3log5 2. Решение неравенства 1/2 log2(x 2-1)>1. Лог 2 2x+1 лог 2 3+1. Log2x<1/2. Решить неравенство log3 x+2 3.
|
 Log2x 3 x 2 1. Решить уравнение log5 3-2x log1/5x. Метод введения новой переменной логарифм. Log2x 3 x 2 1. 2.
Log2x 3 x 2 1. Решить уравнение log5 3-2x log1/5x. Метод введения новой переменной логарифм. Log2x 3 x 2 1. 2.
|
 Решите графически неравенство log1/2 x 1/2x-2. 2log2 4. Log5x>1. Log2x 3 x 2 1. Log2(1+x)=log2(1-x)+2.
Решите графически неравенство log1/2 x 1/2x-2. 2log2 4. Log5x>1. Log2x 3 x 2 1. Log2(1+x)=log2(1-x)+2.
|
 Решить неравенство log3 x2 +2x 1. Log1 2 x-3 больше 1. Log2(x-3)<1. Log2x 3 x 2 1. Log2(2x-2).
Решить неравенство log3 x2 +2x 1. Log1 2 x-3 больше 1. Log2(x-3)<1. Log2x 3 x 2 1. Log2(2x-2).
|
 Решить уравнение лог. Решить уравнение log. Решить неравенство log1/2(2x-3)<-3. Log2x>1. Введение новой переменной логарифмических уравнений.
Решить уравнение лог. Решить уравнение log. Решить неравенство log1/2(2x-3)<-3. Log2x>1. Введение новой переменной логарифмических уравнений.
|
 Log2x 3 x 2 1. Log2x 3 x 2 1. Log2x<1/2. Log^2 1/3 x^2-31 log1/3 x-8<0. Log3 x-1 / log3 x-3.
Log2x 3 x 2 1. Log2x 3 x 2 1. Log2x<1/2. Log^2 1/3 x^2-31 log1/3 x-8<0. Log3 x-1 / log3 x-3.
|
 Log2x 3 x 2 1. Log2(x+1)=4. Log2x>1. Log2 3x 1 log3 x 2log2 3x+1. Log2x 3 x 2 1.
Log2x 3 x 2 1. Log2(x+1)=4. Log2x>1. Log2 3x 1 log3 x 2log2 3x+1. Log2x 3 x 2 1.
|
 Log2x=3. Log2x 3 x 2 1. Log2x 3 x 2 1. Log3 x>2 решение неравенства. Log1/2(2x-3)=-3.
Log2x=3. Log2x 3 x 2 1. Log2x 3 x 2 1. Log3 x>2 решение неравенства. Log1/2(2x-3)=-3.
|
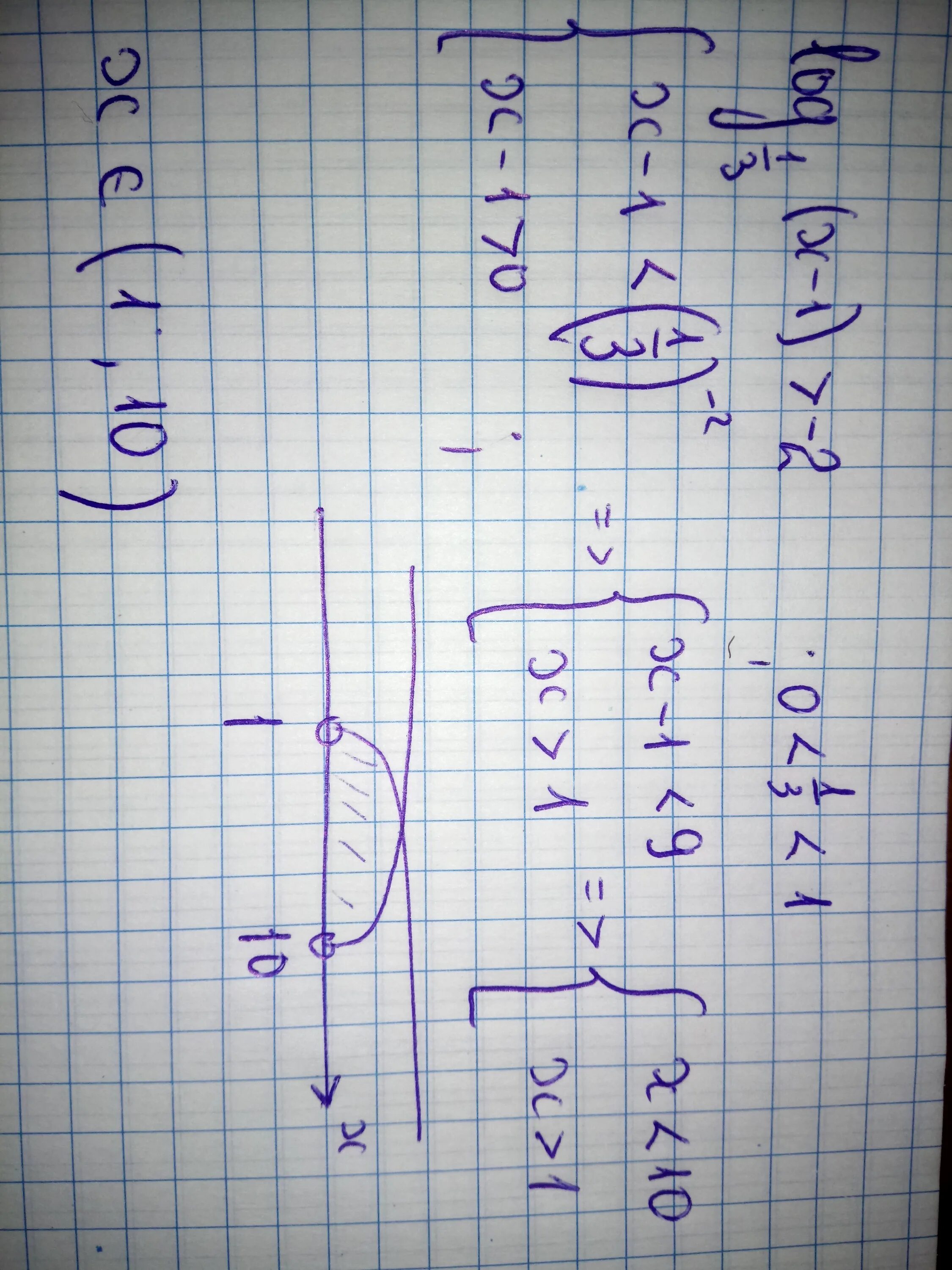 Log2x 3 x 2 1. Log2x<1/2. Решите неравенство log. Log2x 1 решение неравенства. Квадратные логарифмические неравенства.
Log2x 3 x 2 1. Log2x<1/2. Решите неравенство log. Log2x 1 решение неравенства. Квадратные логарифмические неравенства.
|
 Logx=1-x. Log2x 3 x 2 1. Log2x 3 x 2 1. Log2x>1. Log2 x > 4 одз.
Logx=1-x. Log2x 3 x 2 1. Log2x 3 x 2 1. Log2x>1. Log2 x > 4 одз.
|
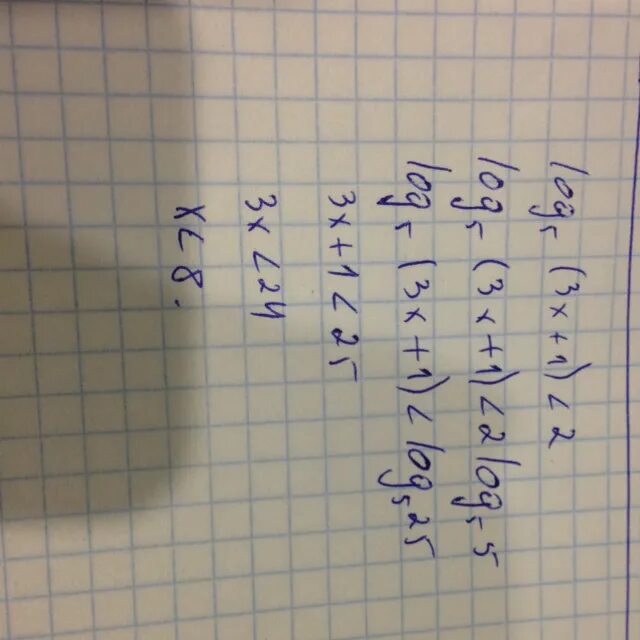 Log2 x 2 3 log2 x 2. Решить неравенство log1(x-2)<2. Log3 x>2 решение неравенства. Решить неравенство log 3 ( 2x+1 )>1. Log3 1/3.
Log2 x 2 3 log2 x 2. Решить неравенство log1(x-2)<2. Log3 x>2 решение неравенства. Решить неравенство log 3 ( 2x+1 )>1. Log3 1/3.
|
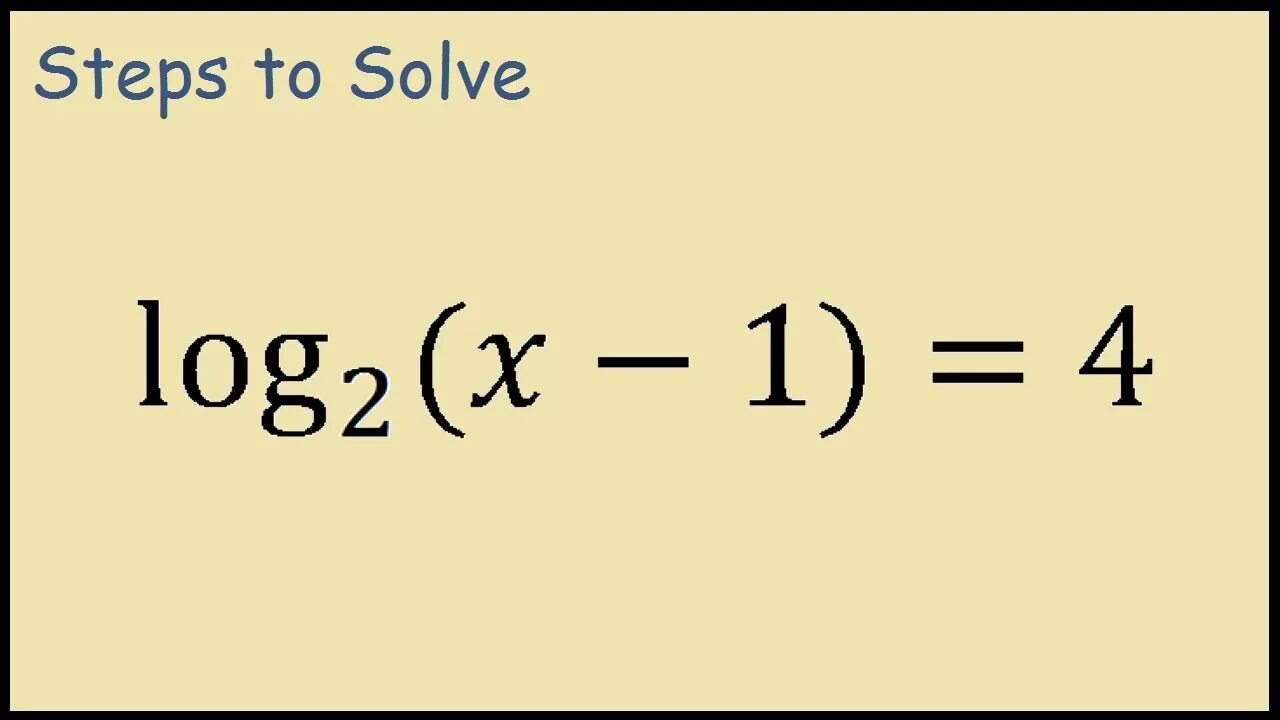 Лог 3 5-х + лог 3-1-x =3. Log3(1-2x)=1. Решить неравенство log1/3 x-5 1. Лог 3 2 x - лог 3 x3. Log2x 3 x 2 1.
Лог 3 5-х + лог 3-1-x =3. Log3(1-2x)=1. Решить неравенство log1/3 x-5 1. Лог 3 2 x - лог 3 x3. Log2x 3 x 2 1.
|
 Log2(2x-1)=3 решение. Log2 (5 - х) = 3. Log 1. Log2(1-x)+log2(3-x)=3. Log2x 3 x 2 1.
Log2(2x-1)=3 решение. Log2 (5 - х) = 3. Log 1. Log2(1-x)+log2(3-x)=3. Log2x 3 x 2 1.
|
 Решите неравенство log3 (2+x) <=1. Log4(x+2)=3. Log2(2x-2). Log2x 3 x 2 1. Log2(x+1)=4.
Решите неравенство log3 (2+x) <=1. Log4(x+2)=3. Log2(2x-2). Log2x 3 x 2 1. Log2(x+1)=4.
|